Kapitel 10 Einführung

Das Paket ggplot2 verwendet eine speziell Systematik beim Erzeugen von Grafiken. Diese basiert auf

Wilkinson (2005): The Grammar of Graphics, Springer.

Kurz gesagt, ist die zugrunde liegende Idee, dass eine statistische Grafik eine Abbildung von Daten auf ästhetische Attribute (Farbe, Form, Größe) von geometrischen Objekten (Punkte, Linien, Balken) ist.

Ferner kann eine Grafik auch noch statistische Transformationen der Daten enthalten. Über die Verwendung verschiedener Facetten ist es möglich dieselbe Darstellung für verschiedene Untergruppen des Datensatzes zu erzeugen.

Am Ende ist es eine Kombination dieser unabhängigen Komponenten, die eine Grafik ausmacht.

Wie immer, laden wir zu Beginn

Man weiß ja vorher nie so genau was man alles so braucht.

library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

10.1 Idee

Die grundlegende Idee des ggplot2 Ansatzes zum Erstellen von Grafiken, besteht darin die Bausteine (verschiedene Layer) eines Plots unabhängig voneinander zu definieren und diese dann zu einer Grafik zusammenzufügen. Eine Grafik besteht immer aus:

• den Daten (als data.frame oder tibble), die ihr visualisieren möchtet

• einer Reihe von Zuordnungen (einem mapping), die beschreiben, wie Variablen aus dem Datensatz auf ästhetische Attribute abgebildet werden

• geometrischen Objekten (geoms), die beschreiben was man am Ende wirklich sieht, also z.B. Punkte, Linien, …

• einem Koordinatensystem, das beschreibt, wie die Koordinaten der Daten auf die Ebene der Grafik abgebildet werden. Außerdem stellt es Achsen und Gitternetzlinien zur Verfügung, die das Lesen der Grafik ermöglichen. Normalerweise verwenden wir ein kartesisches Koordinatensystem, aber es gibt natürlich auch noch eine Reihe anderer Optionen.

• Skalen (scales), die Werte der Daten abbilden auf Werte in einem ästhetischen Raum, sei es in Farbe, Größe oder Form.

Zusätzlich kann die Grafik aber auch noch

• statistische Transformationen (stat), die eine Zusammenfassung der Daten visualisieren,

• Facetten, die es ermöglichen dieselbe Darstellung für verschiedene Untergruppen des Datensatzes zu erzeugen,

• …

enthalten.

Die einzelnen Teile eines Plots werden mit dem + Operator zusammengefügt. Initialisiert wird ein Plot mit ggplot(). Ohne weitere Bestandteile wird aber nur eine leere Grafik erzeugt

library(gapminder)
ggplot(gapminder) 

In den folgenden Abschnitten lernen wir daher wie weitere Bestandteile zum Plot hinzugefügt werden.

10.2 Ein einfacher Scatterplot

Wir schauen uns zum Start einfach mal für Deutschland den Verlauf des gdpPercap über die Zeit an.

gapminder |> 
  filter(country == "Germany") |>  # auswählen der Daten 
  ggplot(aes(x = year, y = gdpPercap)) +  # Plot initialisieren
  geom_point() # Punkte zum Darstellen der Daten verwenden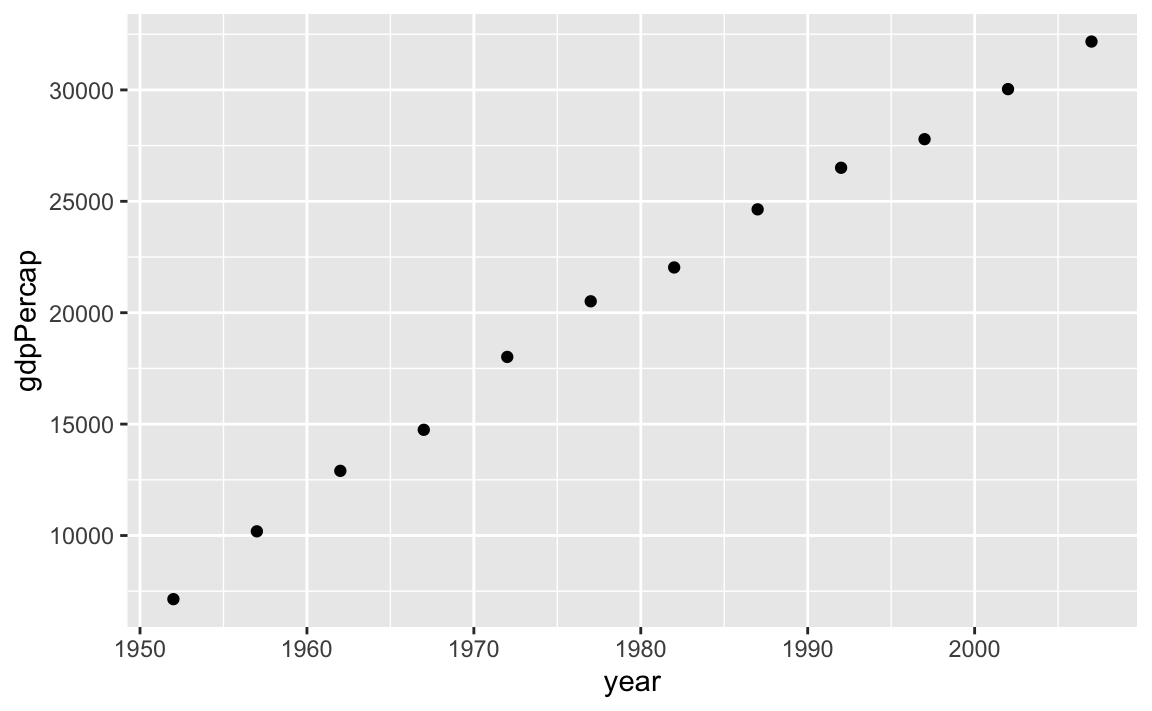

In dieser Grafik haben wir über geom_point() die Art des geometrischen Objekts gewählt. In diesem Fall Punkte. Wenn uns die Form (shape) der Punkte nicht gefällt, so können wir diese natürlich ändern, z.B. in Dreiecke

gapminder |> 
  filter(country == "Germany") |>  
  ggplot(aes(x = year, y = gdpPercap)) +  
  geom_point(shape = 2) # shape auf festen Wert 2 gesetzt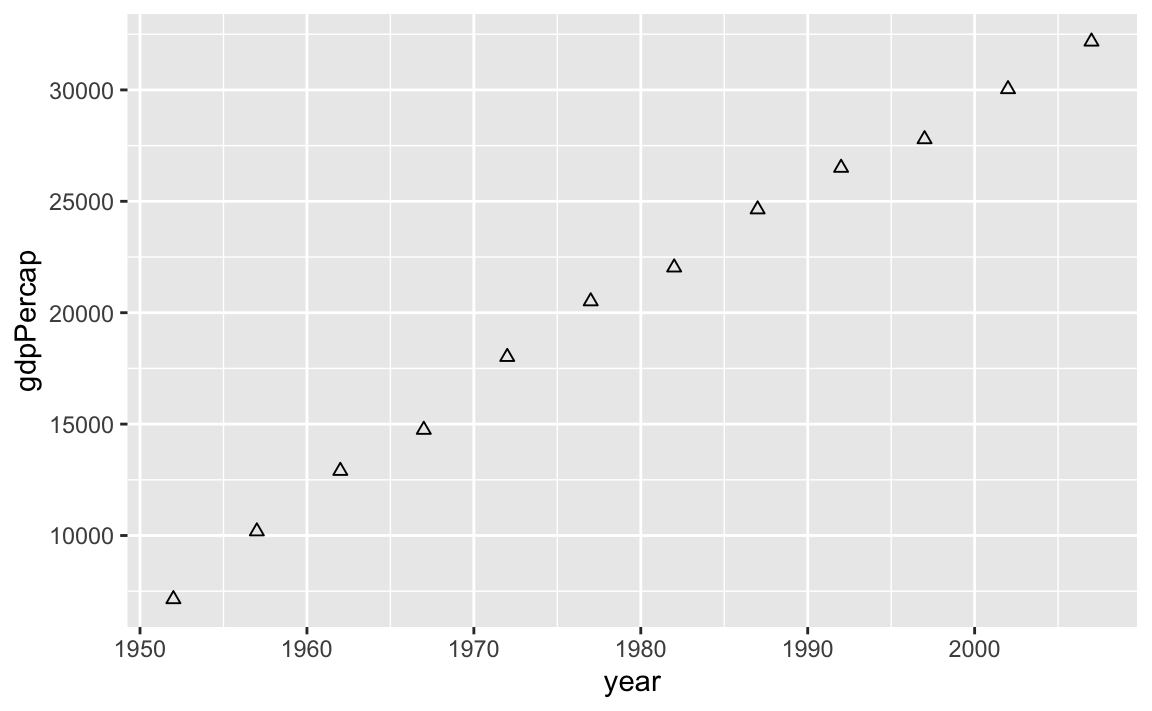

Aber dazu mehr im Abschnitt Scales.

Bemerkung: In diesem einfachen Beispiel haben wir bereits gesehen, dass ggplot() über den Pipe-Operator verknüpft werden kann.